Thermodynamics of Antibody–Antigen
Interactions
The interaction of
antibody and antigen is reversible and can be described by the laws of
thermodynamics. In particular, the reaction
can
be studied and the position of the equilibrium established under varying
conditions. In other words, the amount of anti-body bound to antigen under
different conditions can be estimated. This is crucial information. If
antibody coats a virus then it is likely that the virus will be prevented from
entering target cells and infection will be avoided. If antibody can become
attached to a bacterial cell in a high enough density then complement may be
triggered and the cell killed. The position of equilibrium is described by the
association or binding constant, Ka:
Ka = [Ab Ag complex] / ([Ab] x [Ag])
where
square brackets indicate molar concentrations. The units of Ka are thus
mols per liter, (M−1), or 1/M. If Ka is a large number then
the equilibrium is far to the right and Ab–Ag complex formation is favored.
Typically high‐affinity antibodies have Ka values of the order of 108–1010
M−1. Some researchers prefer to think of binding in terms of a
dissociation constant, Kd, simply defined as 1/Ka
and having the units of M. High‐affinity anti-bodies then have Kd
values of the order of 10−8–10−10 M. As a Kd
= 10−9 M corresponds to 1 nM, high‐affinity antibodies are sometimes
referred to as “nM binders.” Moderate affinity anti-bodies such as IgMs are
often referred to as μM binders (Kd = 1 μM).
Another
way to look at the binding equation is that if half the available antigen
sites are occupied by antibody then [Ag] = [Ab–Ag complex] and Ka =
1/[Ab] or Kd = [Ab]. In other words, Kd is
equal to the antibody concentration at which half of the antibody is bound.
Thus for example a nM binding antibody will begin to complex antigen when its
concentration is in the nanomolar range. The antibody will bind very little if
it is only in the picomolar (10−12) range of concentrations but will bind very
effectively in the μM range. Similarly a μM antibody will be effective in the
μM range of concentration but not the nM. For IgG, nM is roughly 0.15 μg/mL and
mM is 150 μg/mL. The average concentration of IgG in serum is about 12 mg/mL.
Clearly then, if we require that antibodies be present in serum at
concentrations where they are going to be effective in binding antigen, many
many more specificities can be covered by a set of nM binding (high‐affinity)
antibodies than a set of μM binding antibodies. Indeed, this seems to be
largely how Nature operates outside of extreme immunization protocols in animal
models. Thus we are mostly protected, at least against re‐infection following a
primary infection or vaccination, by high‐affinity antibodies at relatively
moderate concentrations.
In the
above discussion, we implicitly assume that antibody–antigen interactions are monovalent,
involving just one Fab arm of the antibody molecule. In fact they may well be
multivalent, which complicates the issues somewhat, but the major points remain
intact. We return to multivalency later.
Binding
constants for antibody–antigen interactions are often estimated from ELISA
measurements but now can be determined
with some precision by techniques such as surface plasmon resonance and
isothermal calorimetry. For binding of antibodies to antigens on the cell
surface, flow cytometry can give a good estimate of binding affinities.
The
binding constant for a reaction is directly related to the energy accompanying
the reaction by the equation:
ΔG = -RT lnKa
where ΔG
is called the free energy of the reaction, R is the gas constant, T
is the temperature in K; and ln is natural log = 2.303 × log10. ΔG is
then another way of describing how far a reaction will be driven to the left or
right at equilibrium under certain conditions. If Ka =109 M−1,
ΔG approx. −12kcal/mol; if Ka = 106 M−1,
ΔG approx. −8 kcal/mol. The advantage of considering the ΔG is
that it can help in beginning to understand the molecular forces that lead to
antibody–antigen interaction. Thus the free energy of a reaction (ΔG )
is the effect of contributions from enthalpy (ΔH ) and entropy :
ΔG = ΔH- T ΔS
The
enthalpy is the heat of the reaction: the more heat is given out by the
reaction (negative ΔH ) the more it will be favored (negative ΔG ).
If heat has to be supplied to the reaction it is disfavored. The more entropy
(or disorder) results from the reaction (positive ΔS ), the more it is
favored. For example, an antibody–antigen interaction would be favored by the
formation of a H bond between the two molecules to the tune of approximately
1–3 kcal/mol. A salt bridge would provide a similar or slightly greater amount
of energy. The reaction would also be favored by hydrophobic surfaces on the
antibody and the antigen coming together because then water that was ordered
around the hydrophobic faces would be released to increase entropy. It is
estimated that burying 1 nm2 of hydrophobic surface generates about 2.5
kcal/mol of binding energy. Some of the forces driving eractions are
summarized in Figure 5.9.
 |
Figure 5.9
Protein–protein interactions. (a) Coulombic attraction between oppositely
charged ionic groups on the two protein side‐chains as illustrated by an
ionized amino group (NH3+) on a lysine of one protein and
an ionized carboxyl group (–COO−) of glutamate on the other. The force of
attraction is inversely proportional to the square of the distance between the
charges. Thus, as the charges come closer together, the attractive force
increases considerably: if we halve the distance apart, we quadruple the
attraction. Furthermore, as the dielectric constant of water is extremely high,
the exclusion of water molecules through the proximity of the interacting
residues would greatly increase the force of attraction. Dipoles on antigen and
antibody can also attract each other. In addition, electrostatic forces may be
generated by charge transfer reactions between antibody and antigen; for
example, an electron‐donating protein residue such as tryptophan could part
with an electron to a group such as dinitrophenyl (DNP) that is electron
accepting, thereby creating an effective +1 charge on the antibody and −1 on
the antigen. (b) Hydrogen bonding between two proteins involving the formation
of reversible hydrogen bridges between hydrophilic groups, such as OH, NH2,
and COOH, depends very much upon the close approach of the two molecules
carrying these groups. Although H bonds are relatively weak, because they are
essentially electrostatic in nature, exclusion of water between the reacting
side‐chains would greatly enhance the binding energy through the gross
reduction in dielectric constant. (c) Nonpolar hydrophobic groups, such as the
side‐chains of valine, leucine, and isoleucine, tend to associate in an aqueous
environment. The driving force for this hydrophobic interaction derives from
the fact that water in contact with hydrophobic molecules with which it cannot
H bond will associate with other water molecules, but the number of
configurations that allow H bonds to form will not be as great as that
occurring when they are surrounded completely by other water molecules (i.e.,
the entropy is lower). The greater the area of contact between water and
hydrophobic surfaces, the lower the entropy and the higher the energy state.
Thus, if hydrophobic groups on two proteins come together so as to exclude
water molecules, between them the net surface in contact with water is reduced
and the proteins take up a lower energy state than when they are separated (in
other words, there is a force of attraction between them). (d) van der Waals
force: the interaction between the electrons in the external orbitals of two
different macromolecules may be envisaged (for simplicity!) as the attraction
between induced oscillating dipoles in the two electron clouds. The nature of
this interaction is difficult to describe in nonmath-ematical terms, but it has
been likened to a temporary perturbation of electrons in one molecule
effectively forming a dipole, which induces a dipolar perturbation in the other
molecule, the two dipoles then having a force of attraction between them; as
the displaced electrons swing back through the equilibrium position and beyond,
the dipoles oscillate. The force of attraction is inversely proportional to the
seventh power of the distance and, as a result, this rises very rapidly as the
interacting molecules come closer together.
An
epitope is often thought of in terms of the region of the antigen contacted by
antibody, a picture provided from crystal structure studies of antibody antigen complexes.
However, it should be borne in mind that looking at contacts between anti-body
and antigen in a crystal structure does not tell us the contributions of
individual interactions to the overall binding energy. This can be done by
measuring the effects of scanning mutagenesis on antibody binding measured. The
available data then suggest that only a few productive interactions
(“hotspots”) dominate the energetics of binding; many interactions are neutral or detrimental to binding even in a high‐affinity antibody antigen pairing. In
the interaction of an antibody with lysozyme, only about a third of the
antibody contact residues actually contribute significantly to net binding
(Figure 5.10).
 |
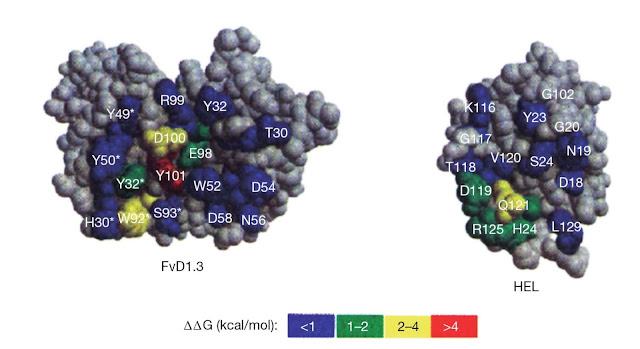Figure 5.10 Energetic map of an
antibody–antigen interface. The antibody D1.3 (single chain Fv (sFv) shown
here) binds with high affinity to hen egg‐white lysozyme (HEL) and
the crystal structure of the complex has been solved (see Figure 5.7). The
energetic contribution of contact residues for both antibody and
antigen can be estimated by substituting the residue with the relatively
“neutral” residue alanine. The effect can be expressed
in terms of the loss of free energy of binding for the interaction on
alanine substitution (ΔΔG). A large positive value for ΔΔG shows
that the alanine substitution has had a strong detrimental effect on binding and
implies that the residue substituted forms a crucial contact in the interface
between antibody and antigen. Clearly, most contact residues,
particularly on the antibody, contribute little to the overall binding energy.
There are clear “hotspots” on both antibody and antigen and the hotspot residues on
the antibody side of the interaction correspond to those on the antigen
side.
A
substitution in only one residue of antigen or antibody can be decisive in net
binding of antibody to antigen. This can be readily appreciated intuitively. If
a bulky residue replaces a small one in the epitope recognized, then the whole
antibody antigen interface may
be disrupted. Pathogens typically evade antibodies by mutations in a small
number of critical residues.
Multivalency in antibody antigen interactions
The
binding of a monovalent Fab fragment to a monovalent antigen can be analyzed in
a straightforward way as described above. This should also be true for the
corresponding divalent IgG molecule interacting with the monovalent antigen.
However, once we consider a divalent IgG (or multivalent anti-body of any
class) interacting with a multivalent antigen, the analysis of binding becomes
more complex.
Consider
IgG binding to an antigen that is expressed as multiple copies on a cell
surface. If the antigen molecules are appropriately spaced and in an
appropriate orientation, IgG may be able to bind divalently (Figure 5.11). This
will lead to a higher affinity (often referred to as the avidity or functional
affinity) of the IgG for the cell surface than the corresponding Fab. The
“bonus effect” of divalent binding can be understood intuitively in terms of
the tendency of the divalent IgG to stick better to the cell surface than the
corresponding Fab. For the Fab to “fall off ” the cell, a series of interactions between
a single antibody combining site and the antigen must be broken. For the IgG to
fall off, the interactions in two antibody combining sites must be broken
simultaneously; a lower probability event. The bonus effect can be thought of
in terms of ΔG. Divalent binding will produce a more favorable ΔH because
of the use of two antibody combining sites. However, an entropy price will be
paid in constraining the Fab arms of the IgG molecule. The net effect in ΔG usually
corresponds to an enhanced affinity of the order of 1‐ to 100‐fold as the bonus
effect. It should also be borne in mind that IgG may bind monovalently even to
a multivalent antigen if the antigen molecules are inappropriately spaced or
oriented. IgM is decavalent for antigen, which in theory could produce a huge
bonus effect in functional affinity. In practice IgMs tend to be rather
moderate affinity binders, suggesting limited use of multivalency and/or a high
entropy price paid for multivalent binding.
 |
Figure 5.11 Divalent antibody binding to
a cell surface. The affinity of an antibody that can bind divalently to a
multivalent antigen (b), such as may be found on a cell surface, is
enhanced relative to an antibody that can only bind monovalently (a).
One of
the most dramatic effects of multivalent antibody interaction can be seen in the neutralization of
toxins. Botulinum neurotoxins cause the paralytic human disease botulism and
are considered a major potential bioterrorist threat. Monoclonal anti-bodies
(mAbs) have been generated from phage libraries against the toxin. No single
mAb protected mice against lethal challenge with toxin. However, a combination
of three mAbs protected mice against a huge challenge with toxin. The
difference could be attributed in part to a multivalency bonus effect
(cooperative binding of the antibodies with more than one molecule of the
toxin) that increased the functional affinities of the antibodies in to the pM
range from the nM range in the individual mAbs. The origins of this effect are
illustrated for a two‐mAb combination in Figure 5.12.
 |
Figure 5.12 The bonus effect of multivalent binding in antibody neutralization of a soluble molecule such as a
toxin. (a–c) It is found that two antibodies binding to non‐overlapping
epitopes on a soluble antigen may show considerably enhanced affinity as
compared to the antibodies used separately (cooperative binding). (d,e) If only
one antibody is present, dissociation of the complex requires only that the
interaction between one antibody combining site and its epitope be disrupted.
(f) If two antibodies are bound to antigen and one antibody‐combining
site–epitope interaction is lost as shown, the complex stays together and the
released Fab arm is in a position to re‐complex. In effect, the koff
values for the two antibodies are decreased in the complex and, if an Fab arm
is dislodged, the
kon
|
